Weil pairing
In mathematics, the Weil pairing is a construction of roots of unity by means of functions on an elliptic curve E, in such a way as to constitute a pairing (bilinear form, though with multiplicative notation) on the torsion subgroup of E. The name is for André Weil, who gave an abstract algebraic definition; the corresponding results for elliptic functions were known, and can be expressed simply by use of the Weierstrass sigma function.
Contents |
Formulation
Suppose E is defined over a field K. Given an integer n > 0 (we require n to be prime to char(K) if char(K)> 0) such that K contains a primitive nth root of unity, then the n-torsion on 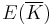 has known structure, as a Cartesian product of two cyclic groups of order n. The basis of the construction is of an n-th root of unity
has known structure, as a Cartesian product of two cyclic groups of order n. The basis of the construction is of an n-th root of unity
for given points ![P,Q \in E(K)[n]](/2012-wikipedia_en_all_nopic_01_2012/I/791a6fc99204b2640076061b91434669.png) , where
, where ![E(K)[n]=\{T \in E(K) \mid n \cdot T = O \}](/2012-wikipedia_en_all_nopic_01_2012/I/e687ffd4ba143c09c65ef7ae8c4cfee7.png) and
and 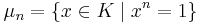 , by means of Kummer theory.
, by means of Kummer theory.
By a direct argument one can define a function F in the function field of E over the algebraic closure of K, by its divisor:
with sums for 0 ≤ k < n. In words F has a simple zero at each point P + kQ, and a simple pole at each point kQ. Then F is well-defined up to multiplication by a constant. If G is the translation of F by Q, then by construction G has the same divisor. One can show that
unless P and Q generate cyclic subgroups one of which is inside the other. In fact then G/F would yield a function on the isogenous curve E/C where C is the cyclic subgroup generated by Q, having just one simple pole. Such a function cannot exist, as follows by proving the residue at the pole is zero, a contradiction.
Therefore if we define
we shall have an n-th root of unity (translating n times must give 1) other than 1. With this definition it can be shown that w is antisymmetric and bilinear, giving rise to a non-degenerate pairing on the n-torsion.
Generalisation to abelian varieties
For abelian varieties over an algebraically closed field K, the Weil pairing is a nondegenerate pairing
for all n prime to the characteristic of k.[1] Here 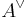 denotes the dual abelian variety of A. This is the so-called Weil pairing for higher dimensions. If A is equipped with a polarisation
denotes the dual abelian variety of A. This is the so-called Weil pairing for higher dimensions. If A is equipped with a polarisation
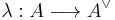 ,
,
then composition gives a (possibly degenerate) pairing
If C is a projective, nonsingular curve of genus ≥ 0 over k, and J its Jacobian, then the theta-divisor of J induces a principal polarisation of J, which in this particular case happens to be an isomorphism (see autoduality of Jacobians). Hence, composing the Weil pairing for J with the polarisation gives a nondegenerate pairing
for all n prime to the characteristic of k.
As in the case of elliptic curves, explicit formulae for this pairing can be given in terms of divisors of C.
Applications
The Weil pairing is used in number theory and algebraic geometry, and has also been applied in elliptic curve cryptography and identity based encryption.
See also
References
- ^ James Milne, Abelian Varieties, available at www.jmilne.org/math/
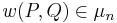
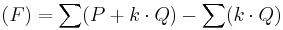
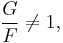
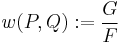
![A[n] \times A^\vee[n] \longrightarrow \mu_n](/2012-wikipedia_en_all_nopic_01_2012/I/4890bd0b6214ccee1570bcbf6663100e.png)
![A[n] \times A[n] \longrightarrow \mu_n.](/2012-wikipedia_en_all_nopic_01_2012/I/89ca42d092f6ed3db4274862397caa77.png)
![J[n]\times J[n] \longrightarrow \mu_n](/2012-wikipedia_en_all_nopic_01_2012/I/531b864742658fc704f609e2968b2bfe.png)